Research
My work is concentrated on dark matter models and possible constraints from observations on small scales. Currently, I am working on a detailed model for the evolution of dark matter substructure. With such a model, we hope to make a precise prediction on the abundance and spatial distribution of subhalos. Combining these predictions with observations on strong gravitational lensing, we will able to get constraints on the property of dark matter.
Previously, I worked on ultralight axion (ULA) dark matter with mass \(\sim 10^{-22}-10^{-21}\) eV. With such a small mass, the de Broglie wavelength of axion particles in dark matter halos can be as large as several kpc. Below this scale, coherent oscillations of ULA dark matter lead to suppression of small-scale structure and could possibly solve the small-scale crisis of the pure CDM model.
To understand the effects of ULA dark matter on small scales, I used two methods:
(1) semi-analytic model (SAM);
(2) direct numerical simulations.
Nonlinear evolution of dark matter subhalos
Under the gravitational interaction, dark matter clusters and forms hierarchical structure, i.e. small halos form first and then merge into large ones. The smaller halo during a merger event become the subhalo of the larger one, the host, and evolve under the tidal field from the host. With semi-analytic models, I am trying to model the orbit, bound mass and density profile evolution of the subhalos by considering variety of physical processes (see a previous paper by Pullen et al. 2014):
(1) Dynamical friction
The host particles passing by close to the subhalo is deflected by the gravity of subhalo, which in turn produce a net drag force on the subhalo. The orbit radius of the subhalo around the host halo thus decays with time.
(2) Tidal stripping
A subhalo is an extensive object. Gravity from the host acted on the subhalo is different at the near side and far side, generating a tidal force that pulls materials away from the subhalo, just like the tide on earth under the influence of the moon. The bound mass of a subhlao decreases due to the mass loss caused by this tidal force.
(3) Tidal heating
The subhalo is usually in an elliptic orbit, so the tidal force acted on it change frequently with time, which heats up the subhalo. The heated subhalo will then expand, leading a decease in its density profile.
Looking at more details in the evolution of a single subhalo, we are trying to improve and extend the previous models for the above effects so that we can make more precise predictions on the statistics of subhalos, e.g. the subhalo mass function.
Semi-analytic model of structure formation with ULA
Simulations of the structure formation in ULA dark matter model with sufficient dynamical range to measure the halo mass function directly are computationally infeasible at present. As an alternative, semi-analytic modelling can be used to compute the properties of galaxies with relative less computational costs.
In the semi-analytic model, synthetic merger trees are first constructed by successively drawing branching events backward in time for a root halo until the halo mass of the progenitors is below the mass resolution. Then halos which have no progenitors are evolved forward in time, taking into account different physical effects such as mergers, dynamical friction and tidal stripping. Finally we get the properties of the host halo at present time.
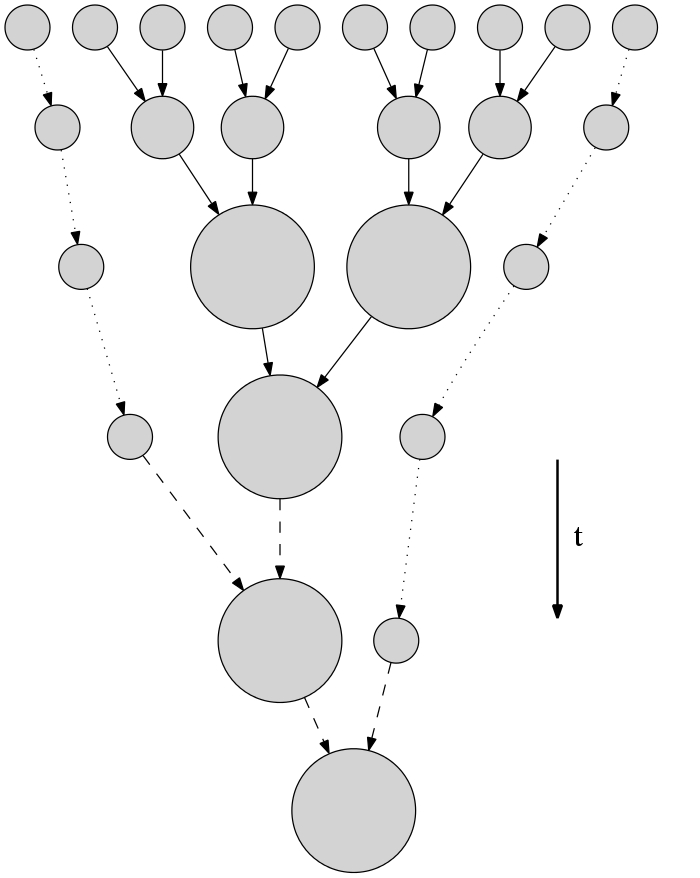
In the past work, we have implemented several aspects of ULA physics in the public semi-analytic code Galacticus:
(1) transfer function with a sharp small-scale cutoff (computed from axionCAMB);
(2) scale-dependent critical overdensity for collapse;
(3) tidal stripping of the subhalo core;
(4) rapid merging of halo cores when when two cores touch.
With the modified Galacticus code, we have analyzed the subhalo mass function of Milky-Way-size ULA dark matter halos. The results has been published in MNRAS.
We also proposed a simplified model to explain the core mass-halo mass relation of ULA halos (which is found in cosmological simulations) and verify the model with our modified semi-analytic code. For details, please take a look at our paper.
The ultimate goal is to obtain constraints on the mass of ULA by comparing the results from semi-analytic model with observations. Currently we are analyzing the gravitational lensing power spectrum from substructure. Corresponding results will be available soon.
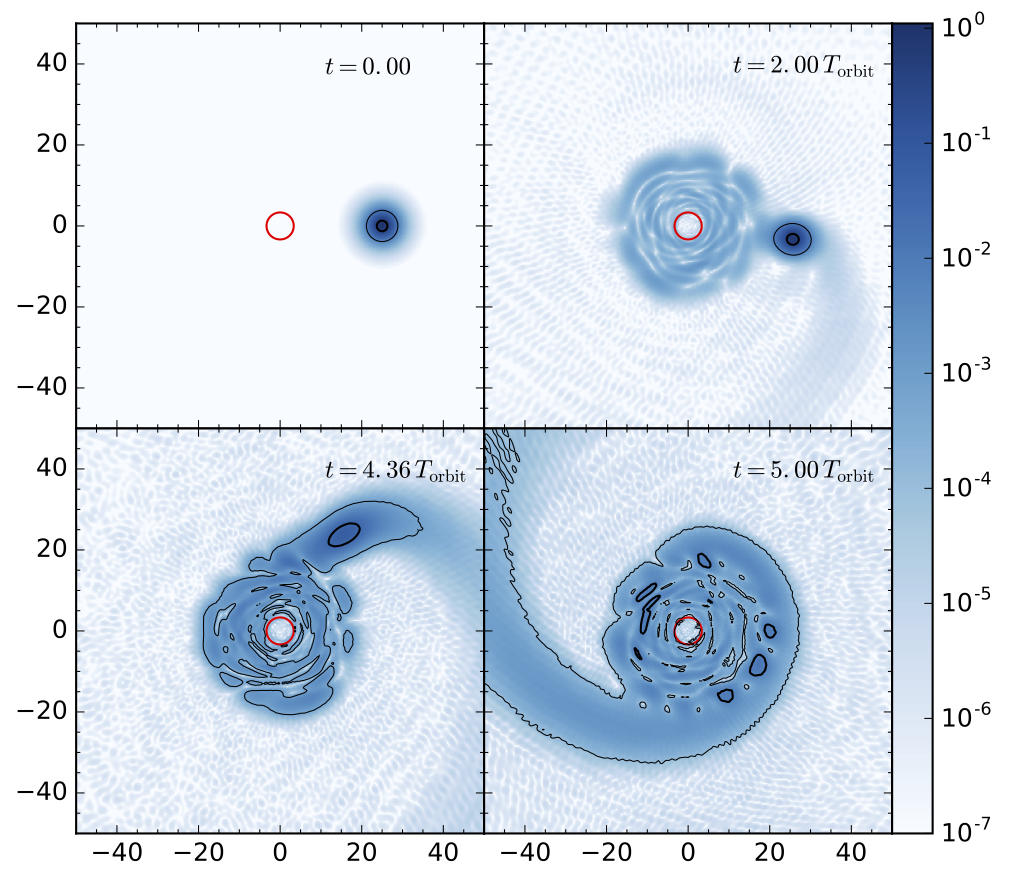
Simulations of tidal disruption of axion subhalo cores
Recently, it is proposed by Hui et al. that the solitonic cores of ULA subhalos are not only subjected to classical tidal stripping, but also subject to an effect they called quantum tunneling. Thus a solitonic core that is stable to classical tidal force will still be stripped out by the tunneling effect in sufficiently long time.
This project aims to study in detail how axion subhalo cores are disrupted and what roles the classical stripping and quantum tunneling play in this process. To perform 3-D simulations of the Schrodinger-Poisson system, a MPI-parallelized forth-order pseudo-spectral solver is developed. Compared to the commonly used leapfrog pseudo-spectral solver, it is about 6 times faster. For details, please take a look at our paper.